“MicroMV 距离解算”的版本间的差异
(→综合校准算法) |
(→综合校准算法) |
||
| 第29行: | 第29行: | ||
已知物体在摄像头画面中只会变小(被部分遮挡)不会变大,所以在计算阶段分别根据物体的宽度和高度计算出两个距离值。当物体像素宽高比与真实宽高比近似时,两个距离值同样可靠;当物体像素宽高比明显大于真实宽高比时,宽度计算得出的距离值更加可靠;当物体像素宽高比明显小于真实宽高比时,高度计算得出的距离值更加可靠 | 已知物体在摄像头画面中只会变小(被部分遮挡)不会变大,所以在计算阶段分别根据物体的宽度和高度计算出两个距离值。当物体像素宽高比与真实宽高比近似时,两个距离值同样可靠;当物体像素宽高比明显大于真实宽高比时,宽度计算得出的距离值更加可靠;当物体像素宽高比明显小于真实宽高比时,高度计算得出的距离值更加可靠 | ||
| − | [[File:microMVdistanceCaculate4.png|| | + | [[File:microMVdistanceCaculate4.png||600px|center]] |
<source lang="py"> | <source lang="py"> | ||
2018年5月21日 (一) 03:48的版本
基本原理
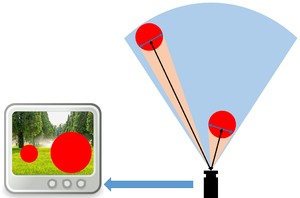
- 本算法依靠近大远小的透视原理,使用物体在画面中的像素宽度结合三角函数计算出物体到摄像头距离。(镜头畸变会影响计算精度)
关键参数
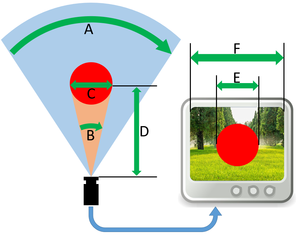
(其中A、C、F是已知常量)
- 摄像头视野范围A度
- 物体占视野B度
- 物体真实宽度C毫米
- 物体距离摄像头D毫米
- 物体占画面像素宽度E
- 摄像头分辨率宽度F
基础距离算法
已知ACEF,首先求出物体占视野角度B
根据:𝐵/𝐴 = 𝐸/𝐹 得到:B=(𝐴∗𝐸)/𝐹
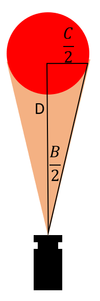
然后求出距离D
根据:tan〖𝐵/2〗 = (𝐶/2)/𝐷 得到:D = 𝐶/(2 tan〖(𝐴∗𝐸)/2𝐹〗 )
综合校准算法
已知物体在摄像头画面中只会变小(被部分遮挡)不会变大,所以在计算阶段分别根据物体的宽度和高度计算出两个距离值。当物体像素宽高比与真实宽高比近似时,两个距离值同样可靠;当物体像素宽高比明显大于真实宽高比时,宽度计算得出的距离值更加可靠;当物体像素宽高比明显小于真实宽高比时,高度计算得出的距离值更加可靠